School District Tax Measures February 11th 2025
Last updated: January 22nd, 2025
As analyses are completed, summary results will be provided on this page.
Contents
- Summary
- Overview
- Local voters’ pamphlet (LVP) statistics
- Bond summary
- Total bond cost to local taxpayers
- Total bond cost to owners of properties with 2024 assessed values of $500,000
- Enrichment levy summary
- Total enrichment levy cost to local property taxpayers in each school district tax area with an enrichment levy measure
- Average annual enrichment levy cost to owners of properties with 2024 assessed values (AVs) of $500,000
- Ranking of the proposed enrichment levies by their percent increases over their previous enrichment levies
- Capital levy summary
- Total capital levy cost to local property taxpayers in each school district tax area with a capital levy measure
- Average annual capital levy cost to owners of properties with 2024 assessed values (AVs) of $500,000
- Total local property taxpayer costs of all measures
- Measure details
- All measures (bonds, enrichment levies, capital levies) by county
- Calculator methodology
- POF proof
Summary
Overview
Listed below are the types and counts for the tax measures for the February 11th 2025 election that have been analyzed to date:
- Bonds: 6
- Enrichment Levies: 45
- Capital / Tech Levies: 19
- Tax measures: 70
- Districts running 1 tax measure: 42
- Districts running 2 tax measures: 14
Local voters’ pamphlet (LVP) statistics
- Bonds
- Number of bonds = 6
- Number of bonds with pro statements = 6
- Number of bonds with con statements = 2
- Number of bonds with phony con statements = 1
- Enrichment, capital and tech levies
- Number of levies = 64
- Number of levies with pro statements = 44
- Number of levies with con statements = 16
LVP pro/con statement statistics by county
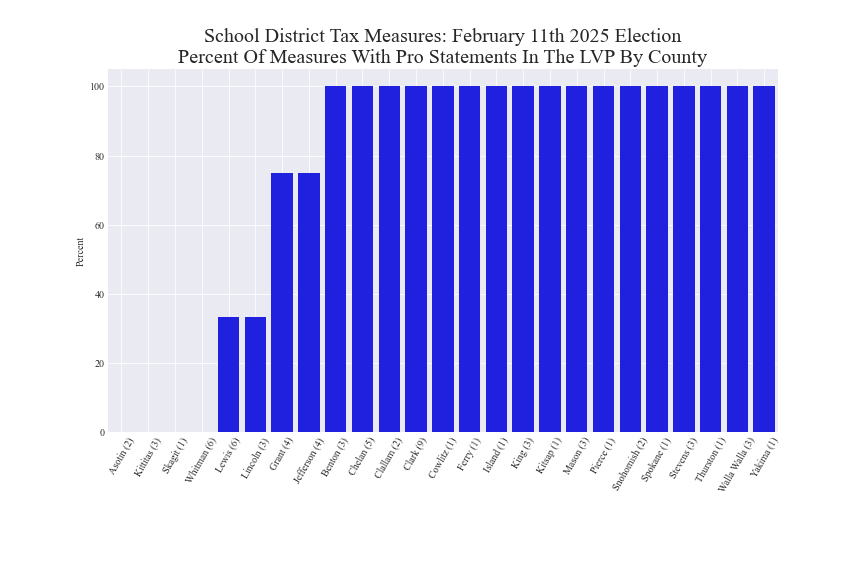
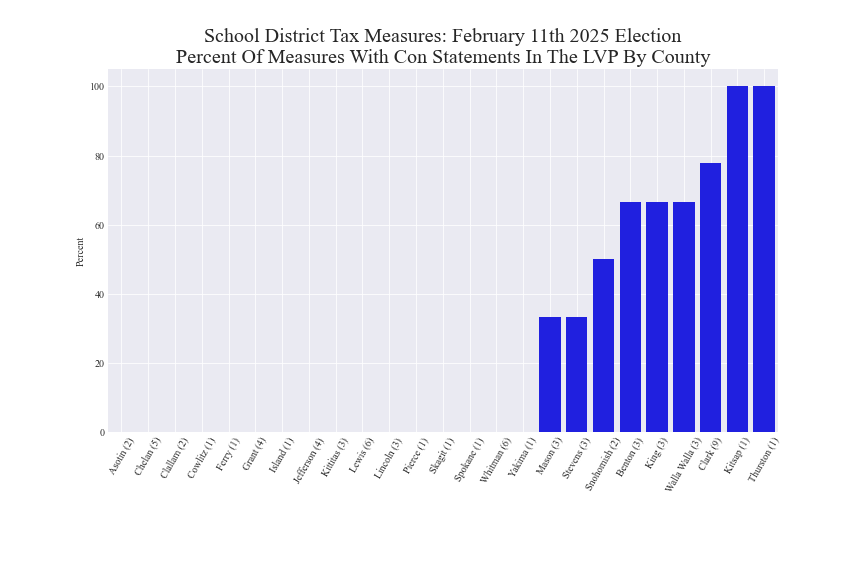
Note: The number of school district tax measures for each county is shown in parentheses.
Bond summary
Total bond cost to local property taxpayers in each school district tax area with a bond measure
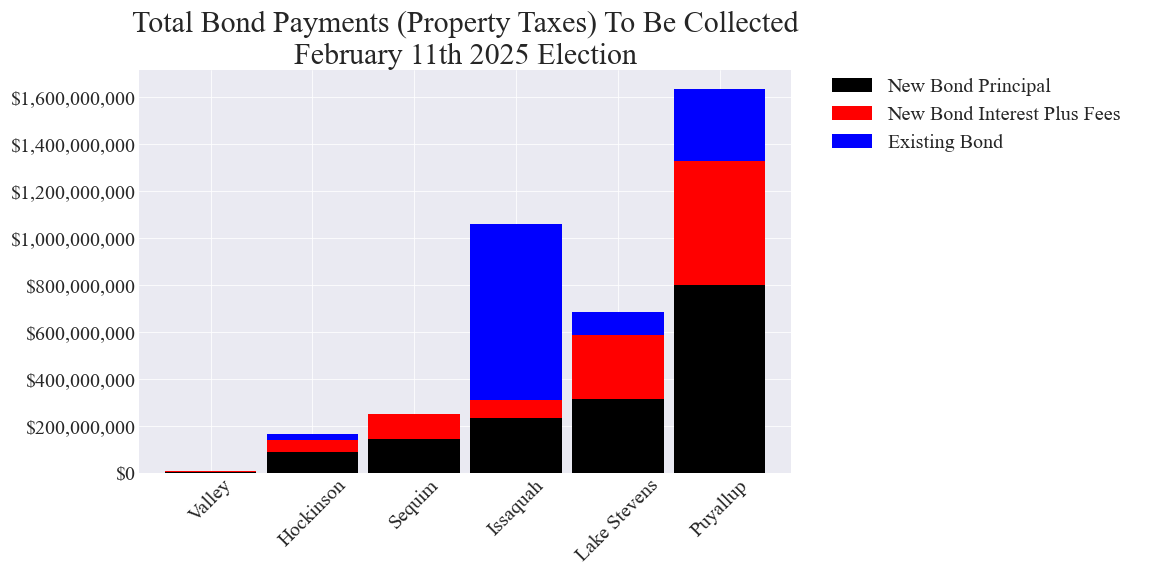
Data source: Each district’s bond/levy projection datasheet
Total bond cost to owners of properties with 2024 assessed values (AVs) of $500,000
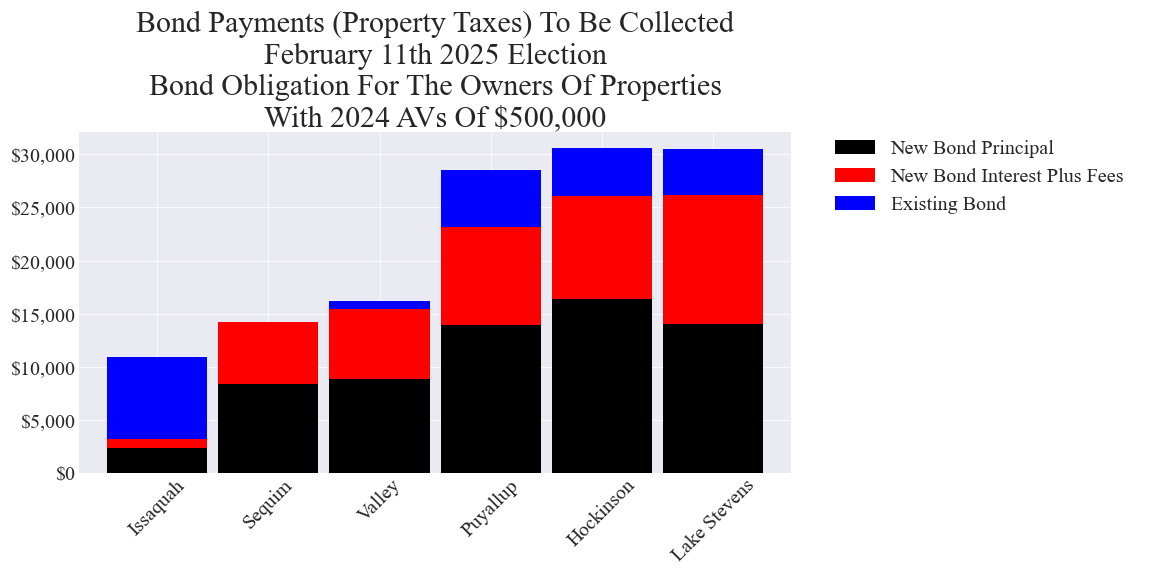
$500,000 was chosen since it is approximately the median of the median home AVs in the school districts with tax measures.
The conservative assumption used was that the POF (proportional obligation factor) as of 2024 remains constant over the term of the bond. The interested reader can use the cost impact estimating calculators (linked below) for the bond and district of interest. An annual POF change parameter can be entered in the calculators as well as different AVs. The county assessor’s office can assist with calculating the historical POF change parameter for any property. The POF = (The example property’s AV for a given year) divided by (The Total AV of all properties in the district’s tax area for the same year).
See the Calculator Methodology section below for more details.
Enrichment levy summary
Total enrichment levy cost to local property taxpayers in each school district tax area with an enrichment levy measure
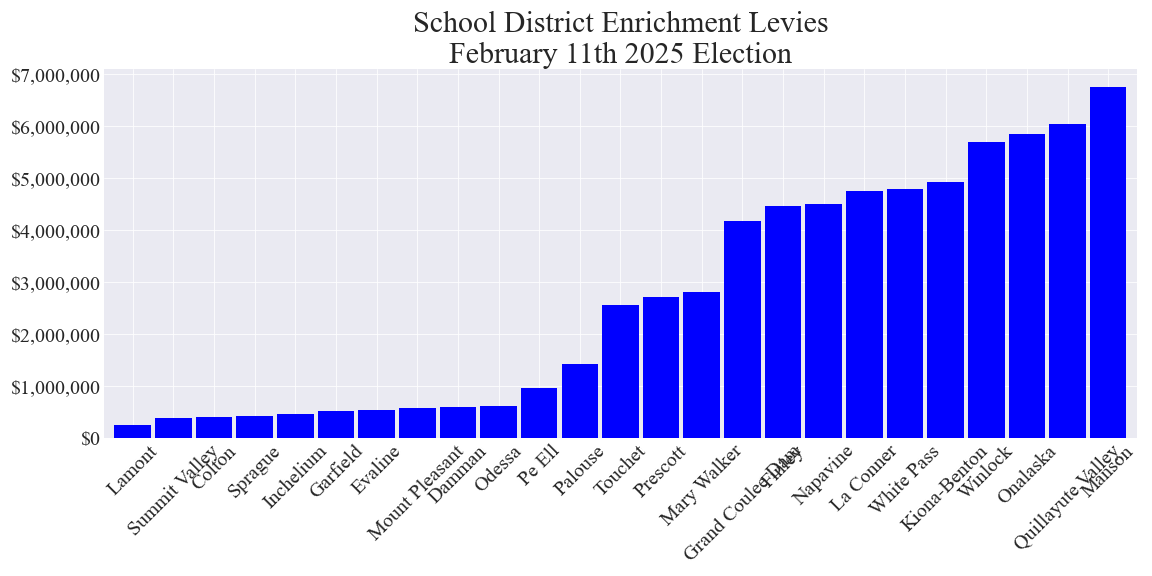
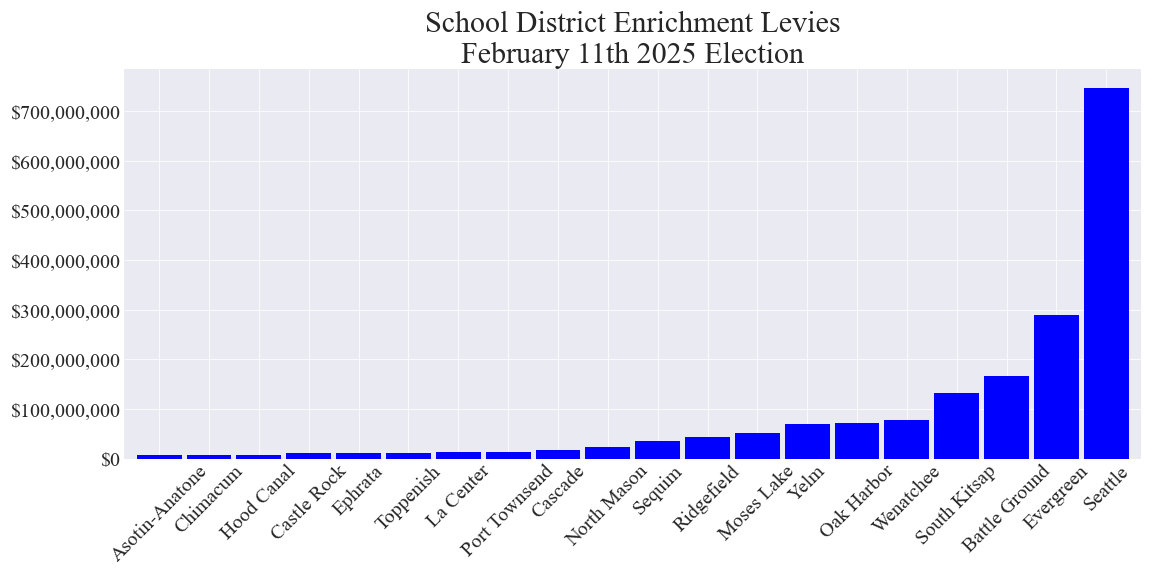
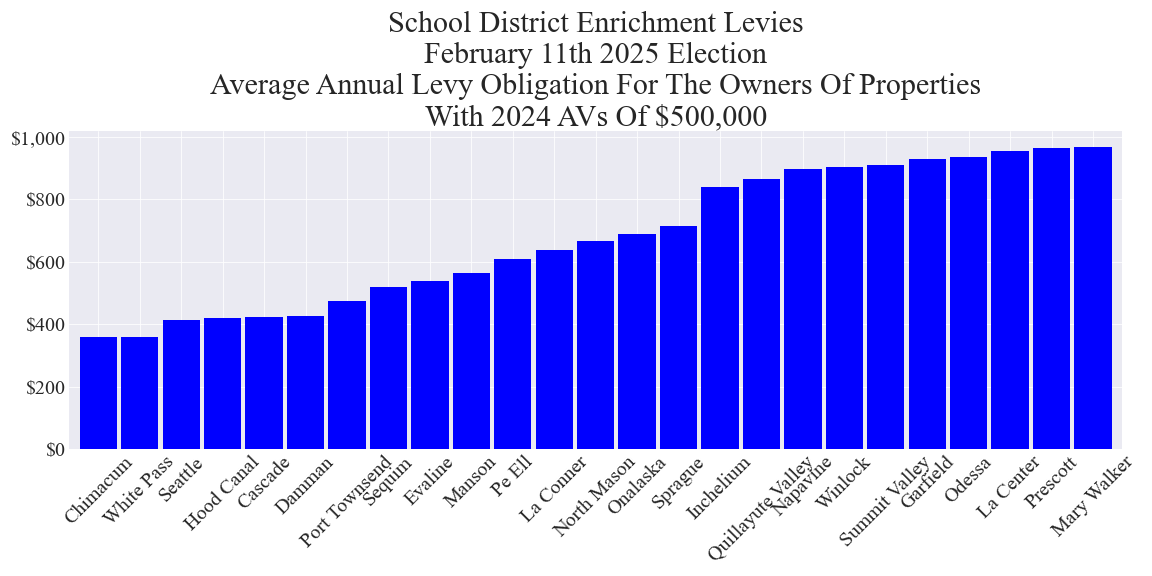
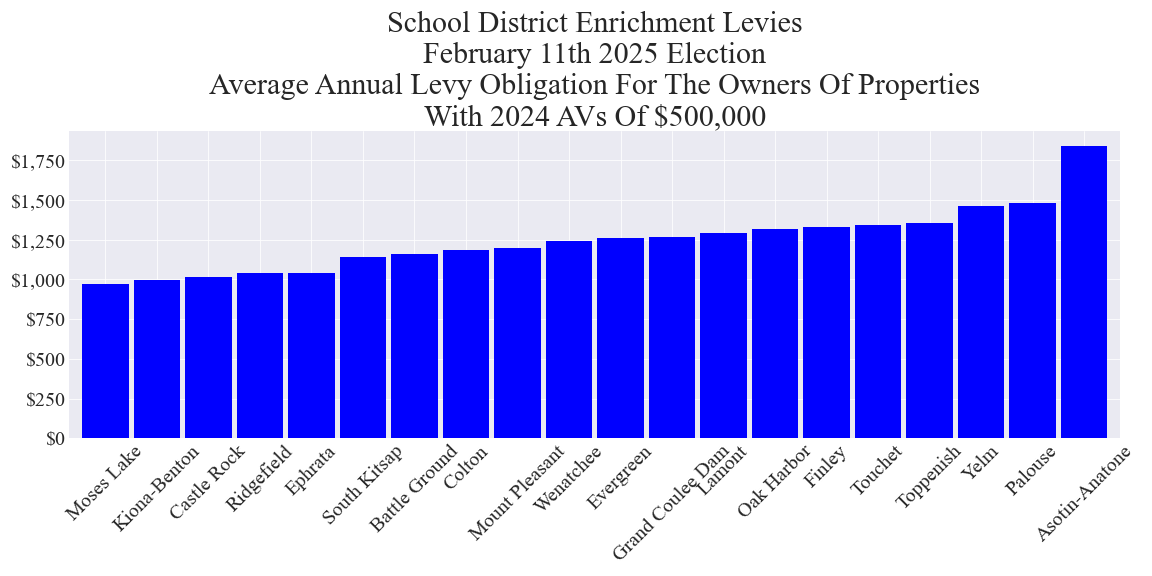
Average annual enrichment levy cost to owners of properties with 2024 assessed values (AVs) of $500,000
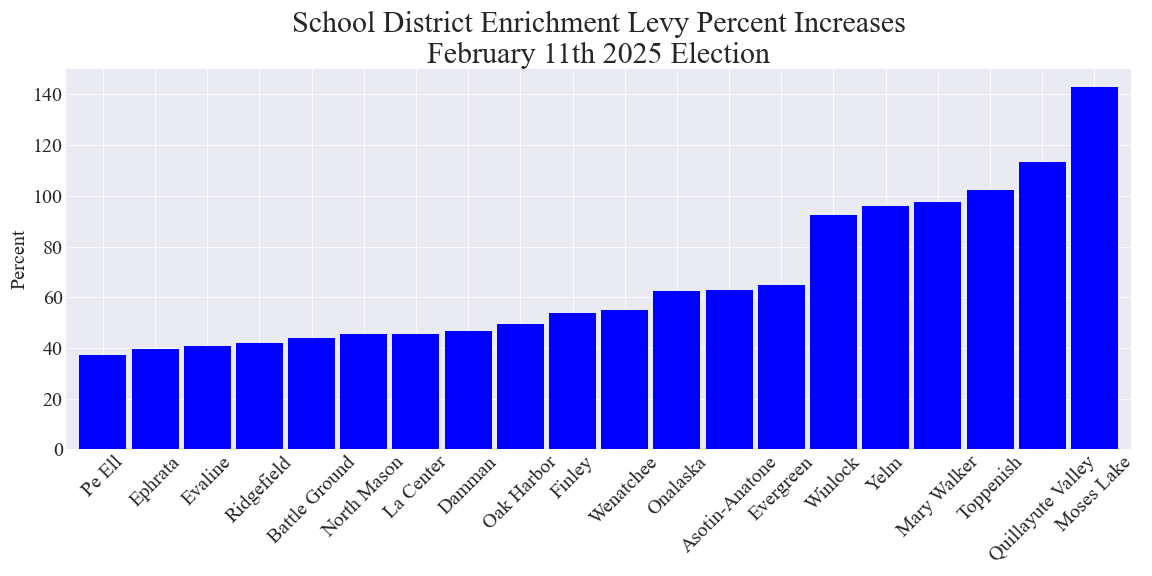
Ranking of the proposed enrichment levies by their percent increases over their previous enrichment levies
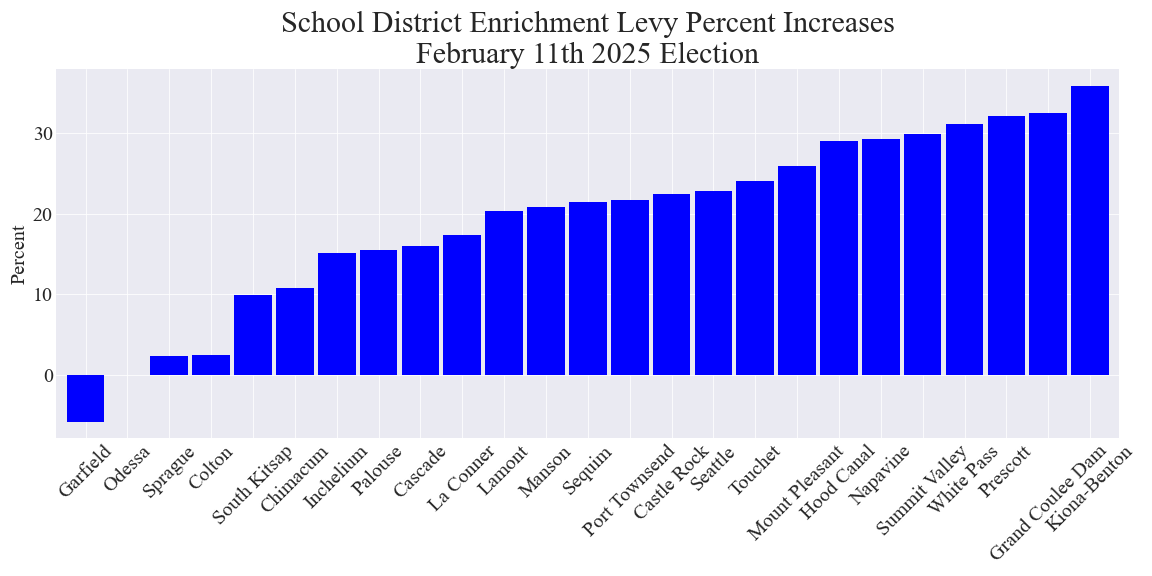
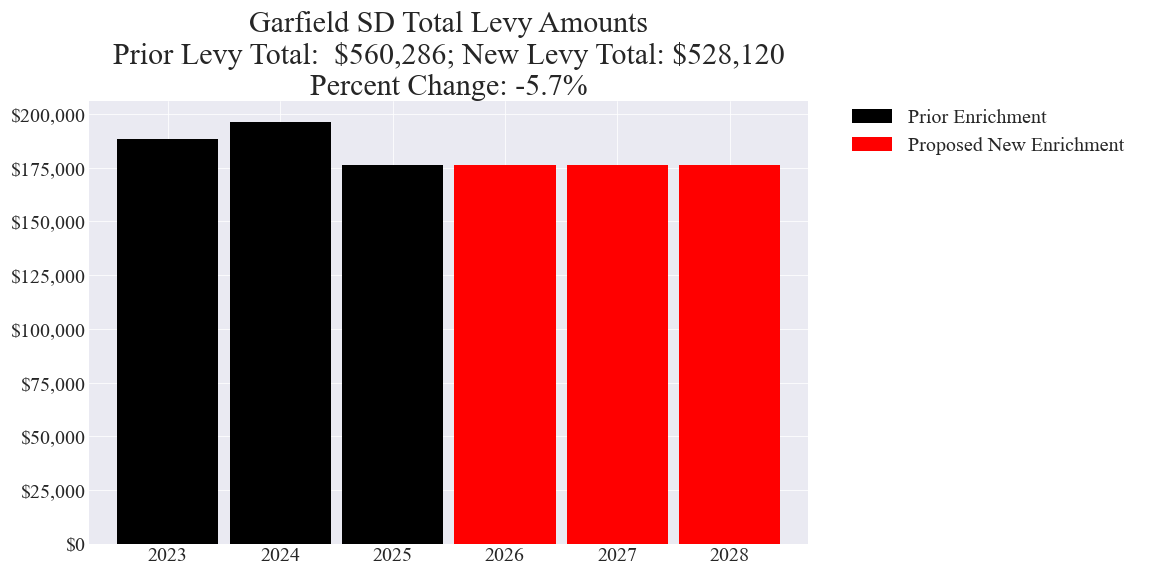
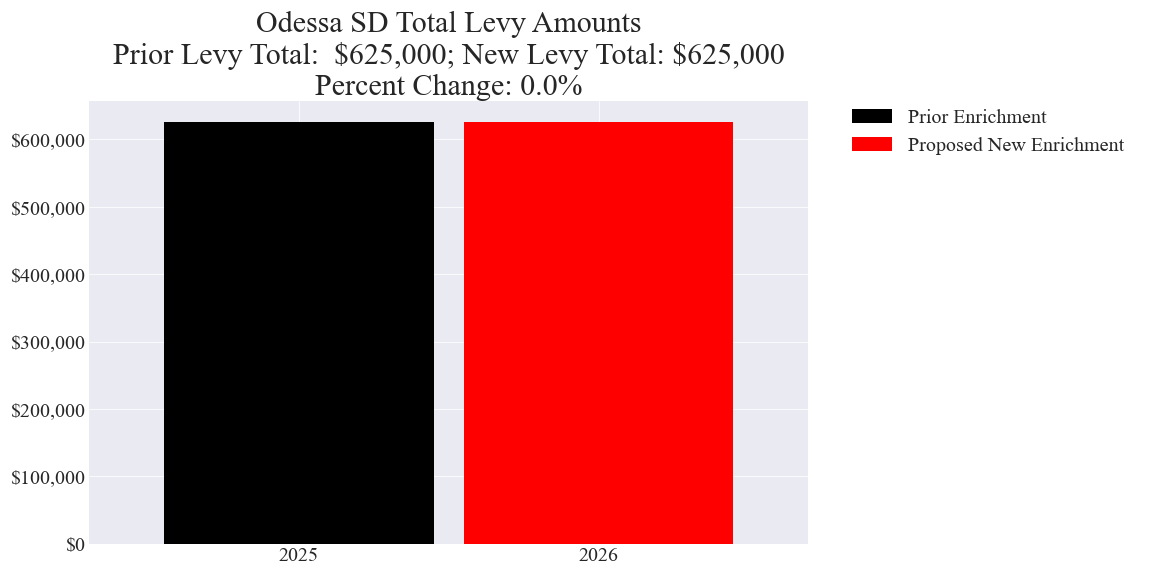
2 examples of enrichment levies with the lowest dollar increases in percent
2 examples of enrichment levies with nearly the highest dollar increases in percent
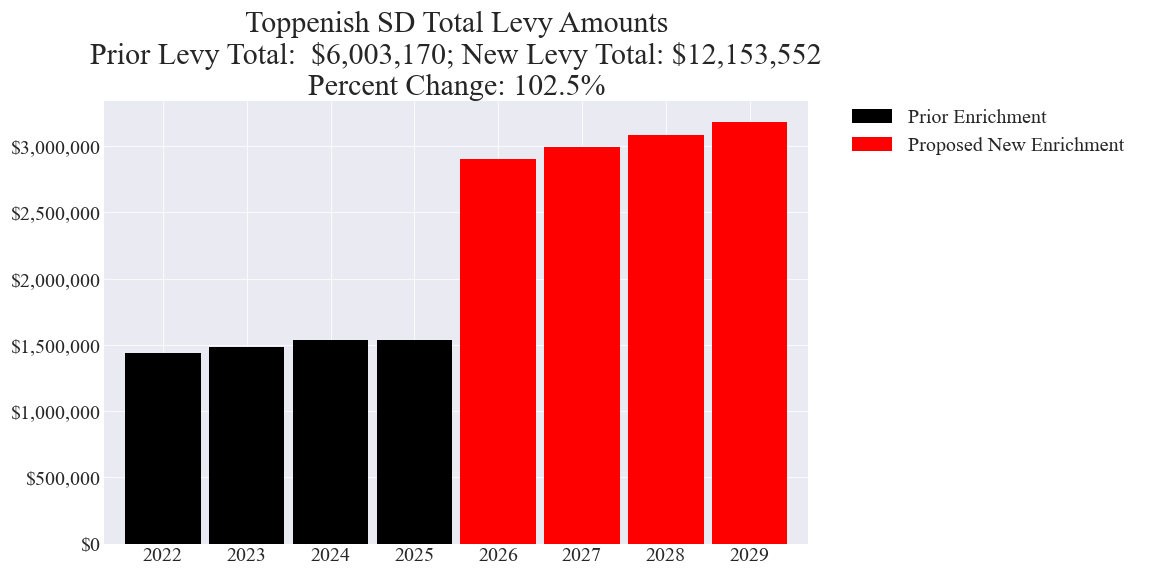
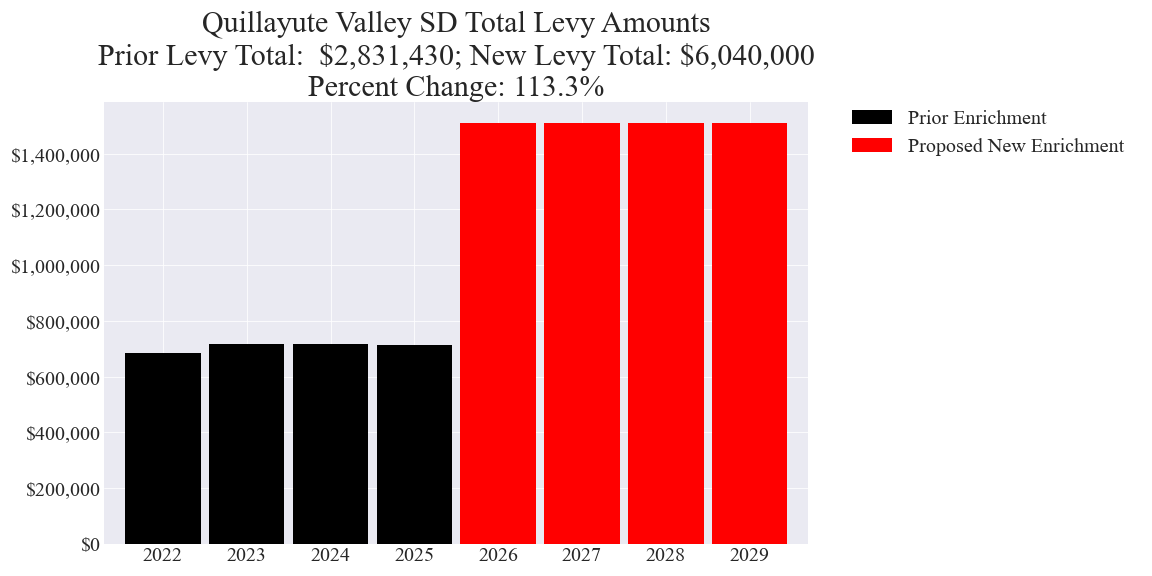
Capital levy summary
Total capital levy cost to local property taxpayers in each school district tax area with a capital levy measure
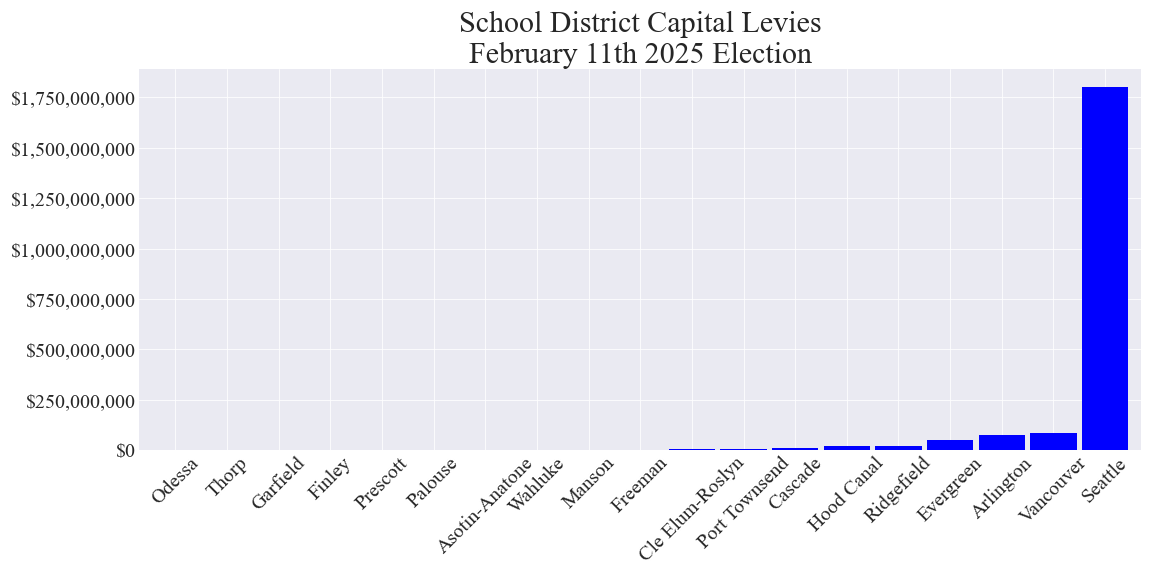
Average annual capital levy cost to owners of properties with 2024 assessed values (AVs) of $500,000
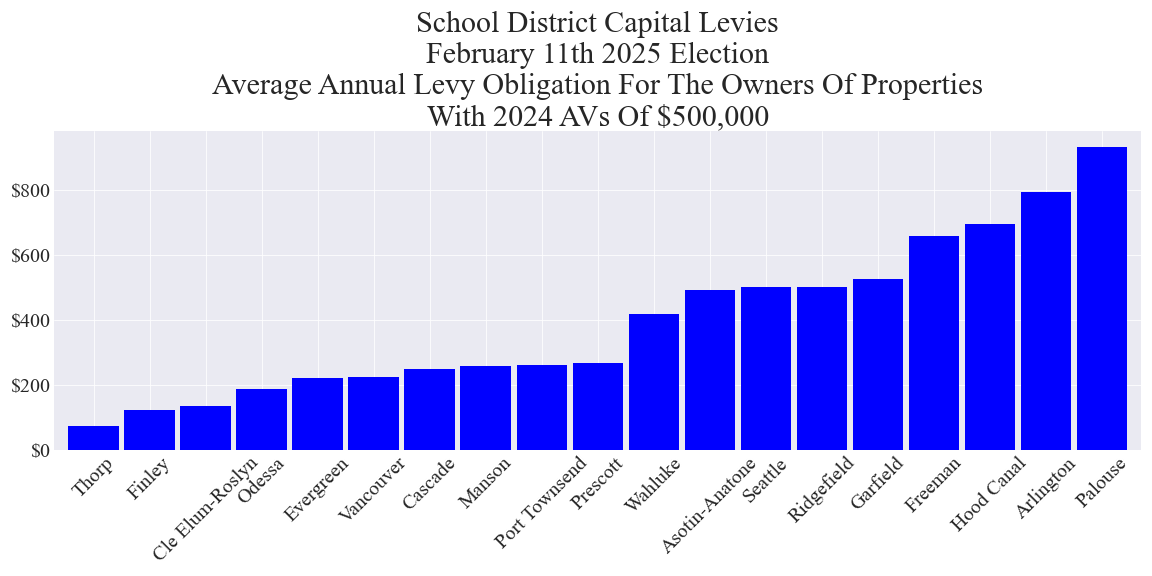
Total local property taxpayer costs of all measures on the ballot
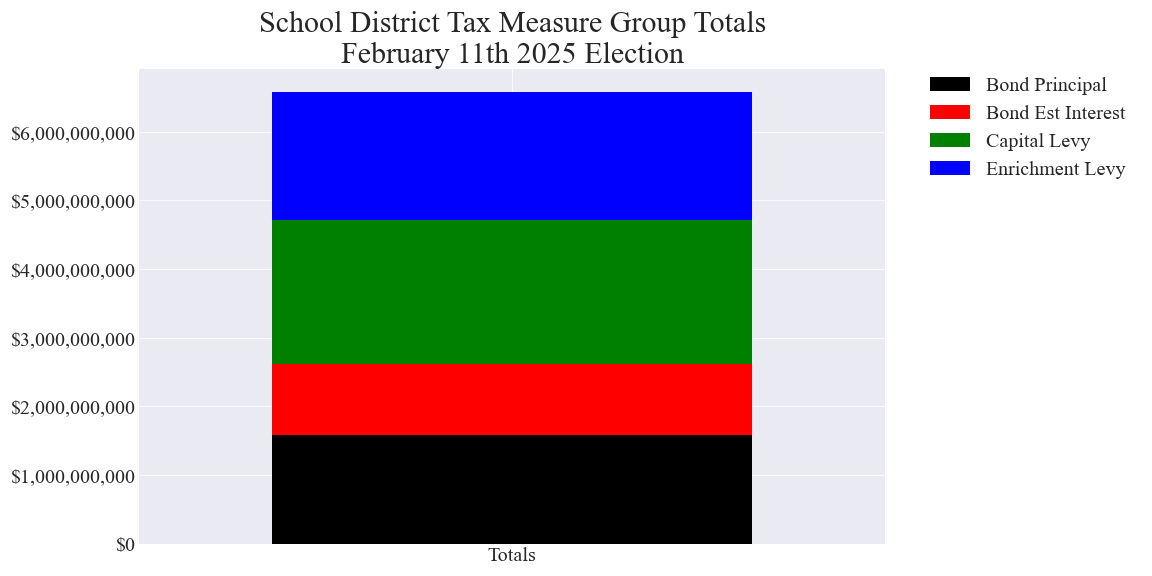
Bonds
Number of bonds: 6
Tax (repayment) durations: 11 – 23 years
Total bond principal: $1.583B
Total bond estimated interest: $1.038B
Total bond principal + estimated bond interest: $2.621B
Capital levies
Number of capital levies: 19
Durations: 1 – 6 years
Total capital levy amount: $2.087B
Enrichment levies
Number of enrichment levies: 45
Durations: 1 – 4 years
Total enrichment levy amount: $1.875B
Capital and enrichment levies
Total levies: $3.962B
Bonds, capital and enrichment levies
Total levies + bonds (principal + interest): $6.583B
Measure details
Tax measures that have been analyzed to date by county
Calculator methodology
School district reps often say they need to correctly guess the future Total AV for their district’s tax area for each of the future years of their tax measures. Their assumption is incorrect and ends up misleading voters/taxpayers. And district reps’ incorrect logic also usually leads to underestimating the true costs of their measures to taxpayers.
In contrast, for the property tax impact estimate calculators on this website, the author uses a Proportional Obligation Factor (POF) method.
Using the 2024 Total District Assessed Value (AV), the POF of the example property was calculated:
POF = (2024 Example Property AV) / (2024 Total District AV)
The POF was then multiplied by the total amount that the district expects to collect each year for the duration of the measure in question (bond or levy) to obtain the estimated taxes for the example property for the measure.
Using this methodology, it doesn’t matter if all properties increase in AV by 20% or all decrease in AV by 20% (which could happen in a recession). The tax collection schedule shown in the charts and tables would still apply for the example property. The example property’s proportion of obligation for the bond debt or levy remains the same over the bond payback or levy period. Tax rates, however, would change. If all properties increase in AV by 20%, the tax rate for the measures would decrease by approximately 20%. If all properties decrease in AV by 20%, the tax rate for the measures would increase by approximately 20%.
Note for the POF annual change parameter for the enhanced calculator versions:
For properties that are increasing in POF (Proportional Obligation Factor), a positive POF annual change will give more accurate results. For properties that are decreasing in POF due to rapid new construction or for other reasons, a negative POF annual change will give more accurate results. However a value of 0 will generally be slightly conservative and will generate estimates that are usually within 5% of actual costs.
It is the author’s opinion that county assessors (in all 39 WA counties), using sound accounting principles, should be providing these calculators for their constituents.
Example calculator calculation:
Centralia SD for their 2023 Enrichment Levy tax measure
Total District AV for 2023: $4,131,948,094
Example property’s AV for 2023: $350,000
POF for 2023 assumed to be the same for years 2023 - 2025: $350,000 / $4,131,948,094 = 8.471E-05
Enrichment Levy amount to collect in 2024: $6,700,000
Example property’s 2024 tax for the Enrichment Levy: POF * (Enrichment Levy amount to collect in 2024) = 8.471E-05 * $6,700,000 = $568
Similarly for the year 2025
Enrichment Levy amount to collect in 2025: $7,600,000
2025 tax = 8.471E-05 * $7,600,000 = $644
POF proof
For any particular future year:
(1) {Tax For An Individual Property For The Year} = {Tax Rate For The Year} X {Property’s AV For The Year}
(2) {Tax Rate For The Year} = {Known Total Tax To Collect For The Year} / {Total AV For The Year}
The apparent problem is that the {Property’s AV For The Year} is not known and the {Total AV For The Year} is not known. That’s 2 unknowns. But we have 2 independent equations. 2 equations, 2 unknowns. Algebra to the rescue.
We can substitute {Tax Rate For The Year} from (2) into (1)
(1a) {Tax For An Individual Property For The Year} = {Known Total Tax To Collect For The Year} / {Total AV For The Year} X {Property’s AV For The Year}
But {POF} = {Property’s AV For The Year} / {Total AV For The Year}
Therefore:
(1b) {Tax For An Individual Property For The Year} = {Known Total Tax to Collect For The Year} X {POF}
POF stays relatively constant for an individual property over many years and regardless of how properties values are rising or falling. The POF for an individual property can be accurately calculated for the current year and used for future years.
Individual properties’ AVs and therefore Total AVs substantially fluctuate from year to year.
This is why even if guesstimated future Total AVs (and therefore future guesstimated tax rates) were accurate, they are not necessary. And worse, future guesstimated tax rates can be set to almost anything by just adjusting the guesses for future Total AVs. Select a higher future Total AV growth, then the future tax rate will be lower. Select a lower future Total AV growth, then the future tax rate will be higher. However, the POF for an individual property does not change as property AVs rise or fall. School districts and other taxing districts should be prohibited from stating their guesstimated future tax rates on their tax measure resolutions and in their campaign materials. That practice misleads voters. School districts, of all institutions, should teach and practice proper logic and mathematics, accurate financial analysis, and ethical behavior.
Voters/taxpayers are voting on amounts in dollars - not guesstimated, inaccurate, future tax rates. This is why TILA (Truth In Lending Act) rules should apply to school district levies and bonds.
If school districts still want to show future rates for their new measures, they should then assume no change in Total AV from the current year and THEN calculate their future rates. Citizens can then calculate their future levy amounts based on the value of their properties’ current year AV.
See the Issaquah SD example bond calculator to demonstrate how future guesstimated tax rates are meaningless:
Link to the Issaquah SD example